Code : Génération et résolution de labyrinthe

Génération d’un labyrinthe par parcours en profondeur

On souhaite construire un labyrinthe, sous la forme d’un graphe dont l’ensemble des sommets est \(\{ (i, j) | 0 \leq i < n, 0 \leq j < p \}\) (une grille rectangulaire de taille \(n \times p\)), et où chaque sommet est adjacent à un ou plusieurs des \(4\) sommets autour de lui.
L’objectif est de trouver un chemin du sommet \((0, 0)\) (en bas à gauche) au sommet \((n - 1, p - 1)\) (en haut à droite).

Pour générer un tel labyrinthe, on peut utiliser un parcours en profondeur sur une grille \(n\times p\) (contenant toutes les arêtes possibles) et où on ne conserve que les arêtes visitées par ce parcours :

import matplotlib.pyplot as plt
import networkx as nx
import random

def generate_labyrinth(n, p):
    G = nx.Graph()
    G.add_nodes_from((i, j) for i in range(n) for j in range(p))
    visited = [[False]*p for _ in range(n)]
    def dfs(i, j):
        visited[i][j] = True
        neighbors = [(i+1, j), (i-1, j), (i, j+1), (i, j-1)]
        random.shuffle(neighbors)
        for x, y in neighbors:
            if 0 <= x < n and 0 <= y < p and not visited[x][y]:
                G.add_edge((i, j), (x, y))
                dfs(x, y)
    dfs(n - 1, 0)
    return G

def draw(G, **keywords):
    plt.clf()
    nx.draw(G, pos={p: p for p in G.nodes()}, node_size=20, **keywords)
    plt.show()

n = 10
G = generate_labyrinth(n, n)
draw(G)

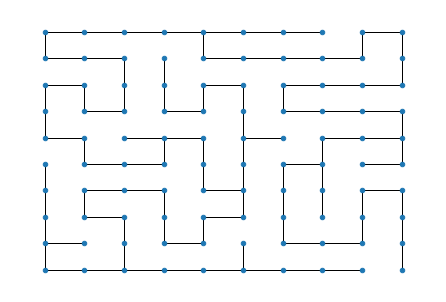
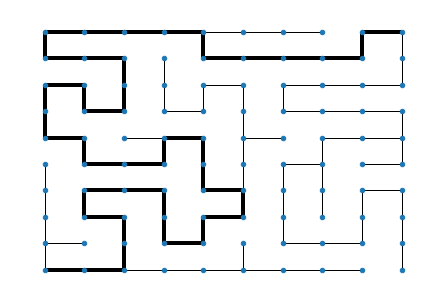
Résolution par parcours en profondeur

Pour trouver un chemin du sommet en bas à gauche au sommet en bas à droite, on peut utiliser un parcours (ici en profondeur) :

def solve_labyrinth(G, n):
    visited = [[False]*n for _ in range(n)]
    path = []
    for i,e in enumerate(G.edges):
        G.edges[e]['index'] = i
    def dfs(i, j):
        if i == n - 1 == j:
            return True
        visited[i][j] = True
        neighbors = [(i+1, j), (i-1, j), (i, j+1), (i, j-1)]
        random.shuffle(neighbors)
        for x, y in neighbors:
            if 0 <= x < n and 0 <= y < n and (x, y) in G[(i, j)] and not visited[x][y]:
                if dfs(x, y):
                    path.append(G[(i, j)][(x, y)]['index'])
                    return True
        return False
    dfs(0, 0)
    return path

path = solve_labyrinth(G, n)
widths = [4 if i in path else 1 for i in range(len(G.edges))]
draw(G, width=widths)

Animation de parcours du labyrinthe

Pour voir dans quel ordre sont considérées les arêtes, on peut utiliser la fonction d’animation suivante :

import networkx as nx
import matplotlib.pyplot as plt
import matplotlib.animation
from IPython.display import HTML

def anim_graph(G, widths):
    fig, ax = plt.subplots(figsize=(20,12))
    plt.close()
    def update(frame):
        ax.clear()
        nx.draw(G, ax=ax, pos={p: p for p in G.nodes()}, node_size=700, width=widths[frame])
    ani = matplotlib.animation.FuncAnimation(fig, update, frames=len(widths), interval=80)
    return HTML(ani.to_jshtml(default_mode="once"))

Animation du parcours en profondeur

On affiche le parcours en profondeur en affichant en gras, à chaque étape, l’arête considérée :

def solve_labyrinth_dfs(G, n):
    widths = [1]*len(G.edges)
    visited = [[False]*n for _ in range(n)]
    frame_widths = []
    for i,e in enumerate(G.edges):
        G.edges[e]['index'] = i
    def dfs(i, j):
        if i == n - 1 == j:
            return True
        visited[i][j] = True
        neighbors = [(i+1, j), (i-1, j), (i, j+1), (i, j-1)]
        random.shuffle(neighbors)
        for x, y in neighbors:
            if 0 <= x < n and 0 <= y < n and (x, y) in G[(i, j)] and not visited[x][y]:
                widths[G[(i, j)][(x, y)]['index']] = 6
                frame_widths.append(widths.copy())
                if dfs(x, y):
                    return True
                widths[G[(i, j)][(x, y)]['index']] = 1
                frame_widths.append(widths.copy())
        return False
    dfs(0, 0)
    return frame_widths

anim_graph(G, solve_labyrinth_dfs(G, n))

Once Loop Reflect

Animation du parcours en largeur

Et voici l’animation du parcours en largeur :

from collections import deque

def solve_labyrinth_bfs(G, n):
    widths = [1]*len(G.edges)
    visited = [[False]*n for _ in range(n)]
    frame_widths = []
    for i, e in enumerate(G.edges):
        G.edges[e]['index'] = i
    q = deque([(0, 0)])
    while len(q) > 0:
        i, j = q.pop()
        if i == n - 1 == j:
            break
        visited[i][j] = True
        neighbors = [(i+1, j), (i-1, j), (i, j+1), (i, j-1)]
        random.shuffle(neighbors)
        for x, y in neighbors:
            if 0 <= x < n and 0 <= y < n and (x, y) in G[(i, j)] and not visited[x][y]:
                widths[G[(i, j)][(x, y)]['index']] = 6
                frame_widths.append(widths.copy())
                q.appendleft((x, y))
    return frame_widths

anim_graph(G, solve_labyrinth_bfs(G, n))

Once Loop Reflect