Animation des parcours

Ce notebook, rédigé en Python, illustre les parcours de graphes (DFS, BFS). Le module cpge utilisé est disponible ici.

Parcours en profondeur

import cpge.graph

G = cpge.graph.random_list() # graphe aléatoire représenté par liste d'adjacence
cpge.graph.draw(G)

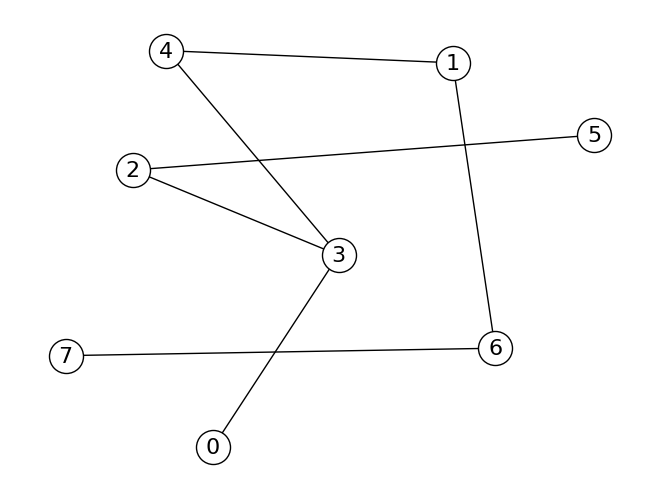
cpge.graph.anim_dfs(G) # parcours en profondeur depuis le sommet 0

Once Loop Reflect

Parcours en largeur

cpge.graph.anim_bfs(G)

Once Loop Reflect

Labyrinthe

Génération par parcours en profondeur

On souhaite générer un labyrinthe parfait (possédant un unique chemin de point à un autre - c’est-à-dire dont le graphe sous-jacent est un arbre) comme celui ci-dessous.
Pour cela, on peut faire partir un parcours en largeur sur un graphe “grille” de taille \(n\times p\) et ne conserver que les arêtes traversées par le parcours.
À chaque appel récursif de dfs, on s’applique aléatoirement sur un des \(4\) voisins qui n’a pas encore été visité.

import matplotlib.pyplot as plt
import networkx as nx
import random

def generate_labyrinth(n, p):
    G = nx.Graph()
    G.add_nodes_from((i, j) for i in range(n) for j in range(p))
    visited = [[False]*p for _ in range(n)]
    def dfs(i, j):
        visited[i][j] = True
        neighbors = [(i+1, j), (i-1, j), (i, j+1), (i, j-1)]
        random.shuffle(neighbors)
        for x, y in neighbors:
            if 0 <= x < n and 0 <= y < p and not visited[x][y]:
                G.add_edge((i, j), (x, y))
                dfs(x, y)
    dfs(n - 1, 0)
    return G

def draw(G, **keywords):
    plt.clf()
    nx.draw(G, pos={p: p for p in G.nodes()}, node_size=20, **keywords)
    plt.show()

n = 10
draw(G := generate_labyrinth(n, n))

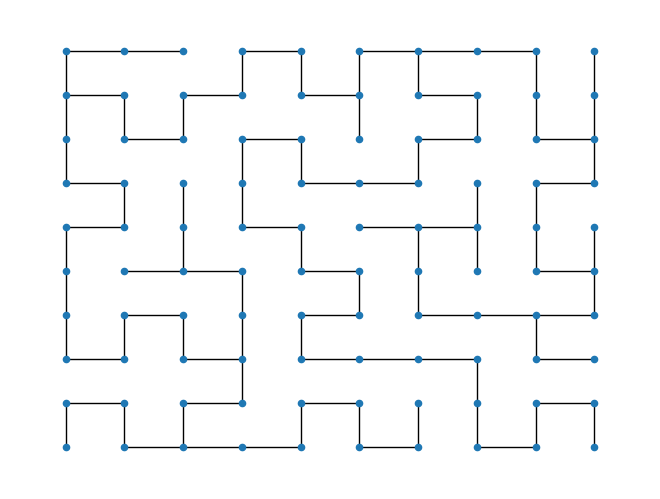
Résolution

Par parcours en profondeur

On cherche maintenant à trouver le chemin de l’entrée (case en bas à gauche) à la sortie (en haut à droite). Pour cela, on effectue encore un parcours en profondeur depuis l’entrée, jusqu’à trouver la sortie :

def solve_labyrinth(G, n):
    visited = [[False]*n for _ in range(n)]
    path = []
    for i,e in enumerate(G.edges):
        G.edges[e]['index'] = i
    def dfs(i, j):
        if i == n - 1 == j:
            return True
        visited[i][j] = True
        neighbors = [(i+1, j), (i-1, j), (i, j+1), (i, j-1)]
        random.shuffle(neighbors)
        for x, y in neighbors:
            if 0 <= x < n and 0 <= y < n and (x, y) in G[(i, j)] and not visited[x][y]:
                if dfs(x, y):
                    path.append(G[(i, j)][(x, y)]['index'])
                    return True
        return False
    dfs(0, 0)
    return path

path = solve_labyrinth(G, n)
widths = [4 if i in path else 1 for i in range(len(G.edges))]
draw(G, width=widths)

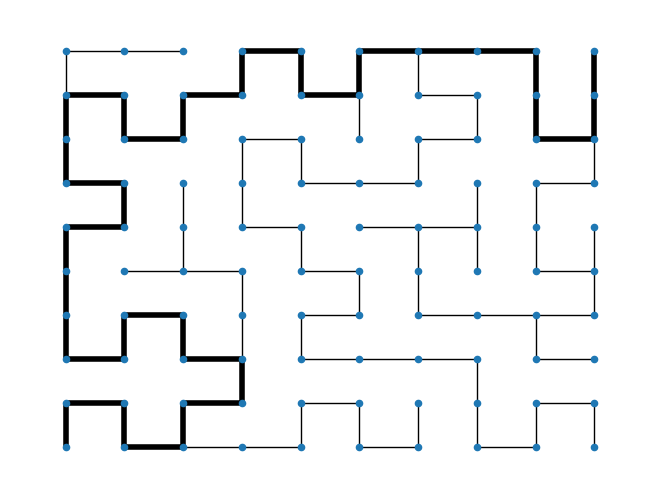
Animation de la résolution du labyrinthe par parcours en profondeur :

import networkx as nx
import matplotlib.pyplot as plt
import matplotlib.animation
from IPython.display import HTML

def anim_graph(G, widths):
    fig, ax = plt.subplots(figsize=(20,12))
    plt.close()
    def update(frame):
        ax.clear()
        nx.draw(G, ax=ax, pos={p: p for p in G.nodes()}, node_size=700, width=widths[frame])
    ani = matplotlib.animation.FuncAnimation(fig, update, frames=len(widths), interval=80)
    return HTML(ani.to_jshtml(default_mode="once"))

def solve_labyrinth_dfs(G, n):
    widths = [1]*len(G.edges)
    visited = [[False]*n for _ in range(n)]
    frame_widths = []
    for i,e in enumerate(G.edges):
        G.edges[e]['index'] = i
    def dfs(i, j):
        if i == n - 1 == j:
            return True
        visited[i][j] = True
        neighbors = [(i+1, j), (i-1, j), (i, j+1), (i, j-1)]
        random.shuffle(neighbors)
        for x, y in neighbors:
            if 0 <= x < n and 0 <= y < n and (x, y) in G[(i, j)] and not visited[x][y]:
                widths[G[(i, j)][(x, y)]['index']] = 6
                frame_widths.append(widths.copy())
                if dfs(x, y):
                    return True
                widths[G[(i, j)][(x, y)]['index']] = 1
                frame_widths.append(widths.copy())
        return False
    dfs(0, 0)
    return frame_widths

anim_graph(G, solve_labyrinth_dfs(G, n))

Once Loop Reflect

Par parcours en largeur

from collections import deque

def solve_labyrinth_bfs(G, n):
    widths = [1]*len(G.edges)
    visited = [[False]*n for _ in range(n)]
    frame_widths = []
    for i, e in enumerate(G.edges):
        G.edges[e]['index'] = i
    q = deque([(0, 0)])
    while len(q) > 0:
        i, j = q.pop()
        if i == n - 1 == j:
            break
        visited[i][j] = True
        neighbors = [(i+1, j), (i-1, j), (i, j+1), (i, j-1)]
        random.shuffle(neighbors)
        for x, y in neighbors:
            if 0 <= x < n and 0 <= y < n and (x, y) in G[(i, j)] and not visited[x][y]:
                widths[G[(i, j)][(x, y)]['index']] = 6
                frame_widths.append(widths.copy())
                q.appendleft((x, y))
    return frame_widths

anim_graph(G, solve_labyrinth_bfs(G, n))

Once Loop Reflect